The missing heritability question is now (mostly) answered

[Jaybee00]

The missing heritability question is now (mostly) answered

Not with a bang but with a whimper

theinfinitesimal.substack.com

 

[forestglip]

Very interesting. The details of how the more accurate heritability algorithms work are beyond me. But the blog is saying that twin studies likely almost always far overestimate heritability due to shared environment.

So where does that leave us in terms of “missing heritability”? Ideally we could compare the RDR and SR estimate to estimates from twins in the same exact cohorts and phenotypes. As a rough approximation, I dug up the corresponding Classic Twin Design estimates from the literature for the traits in each study and averaged them: unsurprisingly, they are in the 50-60% range, as is very typically observed in twin studies.

So twin studies produce a ~2x inflated estimate of narrow-sense heritability when compared to molecular estimates that are free of environmental confounding. The mystery of twin heritability comes to an ignoble end: no massive tranche of rare variants, no phantom interactions, just inflation.

Maybe proving Jonathan correct:

The insurance twin study doesn't look plausible. If h2 was 48% I think that would have been clinically obvious. It is a bit hard to know why this one should be so out of line but I am inclined to either ignore it or allow that the others may be missing some rare stuff.

 

[Yann04]

I’m actually quite suprised the twin heritability studies are done on twins who grew up together.

I always assumed it was done on twins seperated at birth to minimise environmental confounders. Though i guess that would be a logistical nightmare, adoption and parents dying is less common than it once was,

 

[ME/CFS Science Blog]

I always assumed it was done on twins seperated at birth to minimise environmental confounders.

I thought they compared identical with non-identical twins, so that environmental confounders are substracted (as they are present in both pairs of twins).

 

[ME/CFS Science Blog]

Counterpoint is this recent paper in Nature, which suggests that we simply need bigger sample sizes and more detailed measurements of all SNPs, including rare ones.

Here we analyse whole-genome sequence (WGS) data from 347,630 individuals with European ancestry in the UK Biobank2,3 to quantify the relative contribution of 40 million single-nucleotide and short indel variants (with a minor allele frequency (MAF) larger than 0.01%) to the heritability of 34 complex traits and diseases. On average across phenotypes, we find that WGS captures approximately 88% of the pedigree-based narrow sense heritability: that is, 20% from rare variants (MAF < 1%) and 68% from common variants (MAF ≥ 1%). We show that coding and non-coding genetic variants account for 21% and 79% of the rare-variant WGS-based heritability, respectively. We identified 15 traits with no significant difference between WGS-based and pedigree-based heritability estimates, suggesting their heritability is fully accounted for by WGS data.

Estimation and mapping of the missing heritability of human phenotypes | Nature

 

[forestglip]

Counterpoint is this recent paper in Nature, which suggests that we simply need bigger sample sizes and more detailed measurements of all SNPs, including rare ones.

I think the point of the blog is that the algorithms in recent studies are considered to be relatively 'complete' pictures of heritability. Here are the three main algorithms being discussed, which converged on similar estimates and found that heritability was far below what twin studies were showing for several traits:

The best approach is to use the random genetic variation within a family by effectively conditioning on the parental genotypes — proposed in a method known as Relatedness Disequilibrium Regression (or RDR). By using within-family variation, RDR is not susceptible to environmental confounding from relatives or through population stratification. By using primarily family “trios” with one child, RDR is inherently immune to biases from sibling environmental relationships. And by drawing most of its signal from the pairs of individuals between different families (after accounting for genetic confounding via their parents), RDR does not pick up environmental or genetic interactions which distant individuals do not share. RDR thus estimates “narrow-sense” heritability in its most well-defined form.

The next best approach is to use the random genetic sharing between siblings — a method known as Sibling Regression (or SR). By using within-family variation, like RDR, SR is not confounded by stratification and shared environment. But because it uses only pairs of siblings, SR has to assume that siblings do not systematically influence each other (no “sibling indirect effects”). And because siblings are not distant relatives, SR will also pick up the influence of within-family gene-gene and gene-environment interactions. So SR estimates something that is between narrow-sense and broad-sense heritability (if you consider broad-sense heritability to include GxE).

The third best approach is to brute force it: simply measure every single mutation in the genome in a large population of unrelated individuals, typically using a whole-genome sequencing (WGS) assay, and then put all of those mutations into one of several well-established GWAS heritability estimators (we’ll call this GREML-WGS2). This approach does not have the advantage of using within-family variation, and therefore will include any environmental influences that are correlated with genetics, such as familial factors or stratification. That means GREML-WGS estimates are essentially untethered from narrow- or broad- sense heritability because they can include entirely non-genetic variance. But many biobank traits, like lipid levels or blood counts, are probably not under the strong indirect influence of parental genetics. So GREML-WGS can act as a crude confirmatory analysis, as well as a way to partition the contribution of measurable rare and common variation.

Long story short, several recent papers have now applied each of these methods to a representative set of complex traits. Young et al. (2018) ran RDR on 14 traits in Iceland, Yengo et al. (2025) ran SR on 14 traits in collaboration with 23andme, and Wainschtein et al. (2025) ran GREML-WGS on 34 traits in the UK Biobank. For any one trait, the estimates are often still much too uncertain and population specific (see below). But across traits, one can get a good sense of where the missing heritability is and where it isn’t:

What it says about continuing to mine for rare variants to identify the missing heritability:

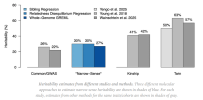
Perhaps a massive tranche of ultra rare variants with massive effects will still explain the difference? There is a tendency to keep looking over the next hilltop for the answer, but this hypothesis has been thoroughly mined. The SR estimates already include the contribution of ultra-rare variants and the RDR estimates include the contribution of many (though not all) ultra-rare variants. Wainschtein et al. also found no contribution from ultra rare variants on average and the previous work of Weiner et al. (2023) estimated the gene burden heritability including ultra-rare variants at just 1.3% on average. Lastly, highly penetrant ultra-rare variants would have been discovered with pre-GWAS linkage analyses powered precisely for this scenario.

 

[ME/CFS Science Blog]

I think the point of the blog is that the algorithms in recent studies are considered to be relatively 'complete' pictures of heritability. Here are the three main algorithms being discussed, which converged on similar estimates and found that heritability was far below what twin studies were showing for several traits:

Ah, so the h^2 pedigree in the Wainschtein et al. (2025) paper already used the lower heritability estimates using those algorithms, not the high estimates from twin and kin studies?

 

[forestglip]

Ah, so the h^2 pedigree in the Wainschtein et al. (2025) paper already used the lower heritability estimates using those algorithms, not the high estimates from twin and kin studies?

Oh I hadn't realized the paper you linked was the same one mentioned in the blog.

I'm not entirely sure. I think they did both the GREML algorithm and more traditional pedigree-based estimates.

I'm confused because the chart in the blog shows a bar for twin-based heritability in Wainschtein, but I don't see the word twin mentioned in the paper. It's really complicated (to me), so I might just not understand this.