So, more just a difference in the timing of the decline – a delay for healthy controls – than a difference in the type or shape of the decline? Meaning patients are just hitting their limits much sooner?If you look at the chart replicated above in post 71, it looks as though the healthy group's line would have kept going down, perhaps following a similar trajectory as the ME/CFS group if everyone had been allowed to continue on with the reps until they were fatigued.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Grip test results and brain imaging in the NIH study: Deep phenotyping of PI-ME/CFS, 2024, Walitt et al
- Thread starter Andy
- Start date
Just want to make sure everyone saw Betsy Keller's response in her recent 2 day CPET paper. She addresses the "not central or peripheral fatigue" claims from an exercise science perspective:
"A recent study of post-infectious ME/CFS (N = 17) and healthy controls (N = 21) assessed a comprehensive panel of physiological, physical, cognitive, biochemical, microbiological, and immunological variables [84]. Of these measures, only 8 ME/CFS and 9 controls completed a single CPET with an average VO2peak about 40% higher in the control group. Based on this small sample size and inappropriately matched control group, authors suggested that impaired ANS function in ME/CFS, evidenced by diminished HRV, abnormal tilt-related symptoms, and other abnormal orthostatic responses, led to lower metabolic energy production and work output, and may be contributed to by a reduced ‘effort preference’. Effort preference was assessed in this study using the Effort-Expenditure for Rewards Task [85], which utilized a small motor task to assess for anhedonia typically associated with major depressive disorder. The Effort-Expenditure for Rewards Task is not highly associated with measures of whole-body oxygen consumption or power output compared to conventional indices of effort (%peak HR, RER, RPE), none of which were reported in the study. Whereas the link between ANS dysfunction and impaired energy metabolism is not inconsistent with the systemic CPET data reported herein, their reasoning is misguided. It has long been known that the magnitude of cardiovascular responses to exertion is predominantly influenced by the relative level of muscle activation (number and intensity of activated muscle fibers) via feedback loop from peripheral interoceptors (e.g., Golgi tendon organs, muscle spindles, etc.) to the motor cortex then to the brainstem [85]. Disruption of this feedback loop at any level, for example, due to infection of the vagus nerve postulated by VanElzakker [86] to emanate from the gut of ME/CFS, would negatively impact this tightly controlled process and downregulate central nervous system signaling of cardiovascular support peripherally for energy production. Consequently, during incremental exercise (i.e., CPET) accumulation of local muscle metabolites from insufficient blood flow coupled with dysregulated central signaling at the brainstem, will directly inhibit the relative level of muscle activation and thereby reduce effort. Given that both ME/CFS and well-matched CTL in the present study achieved similarly high metrics at peak effort during CPET, we saw no evidence of reduced peak effort in ME/CFS."
https://translational-medicine.biomedcentral.com/articles/10.1186/s12967-024-05410-5
"A recent study of post-infectious ME/CFS (N = 17) and healthy controls (N = 21) assessed a comprehensive panel of physiological, physical, cognitive, biochemical, microbiological, and immunological variables [84]. Of these measures, only 8 ME/CFS and 9 controls completed a single CPET with an average VO2peak about 40% higher in the control group. Based on this small sample size and inappropriately matched control group, authors suggested that impaired ANS function in ME/CFS, evidenced by diminished HRV, abnormal tilt-related symptoms, and other abnormal orthostatic responses, led to lower metabolic energy production and work output, and may be contributed to by a reduced ‘effort preference’. Effort preference was assessed in this study using the Effort-Expenditure for Rewards Task [85], which utilized a small motor task to assess for anhedonia typically associated with major depressive disorder. The Effort-Expenditure for Rewards Task is not highly associated with measures of whole-body oxygen consumption or power output compared to conventional indices of effort (%peak HR, RER, RPE), none of which were reported in the study. Whereas the link between ANS dysfunction and impaired energy metabolism is not inconsistent with the systemic CPET data reported herein, their reasoning is misguided. It has long been known that the magnitude of cardiovascular responses to exertion is predominantly influenced by the relative level of muscle activation (number and intensity of activated muscle fibers) via feedback loop from peripheral interoceptors (e.g., Golgi tendon organs, muscle spindles, etc.) to the motor cortex then to the brainstem [85]. Disruption of this feedback loop at any level, for example, due to infection of the vagus nerve postulated by VanElzakker [86] to emanate from the gut of ME/CFS, would negatively impact this tightly controlled process and downregulate central nervous system signaling of cardiovascular support peripherally for energy production. Consequently, during incremental exercise (i.e., CPET) accumulation of local muscle metabolites from insufficient blood flow coupled with dysregulated central signaling at the brainstem, will directly inhibit the relative level of muscle activation and thereby reduce effort. Given that both ME/CFS and well-matched CTL in the present study achieved similarly high metrics at peak effort during CPET, we saw no evidence of reduced peak effort in ME/CFS."
https://translational-medicine.biomedcentral.com/articles/10.1186/s12967-024-05410-5
ME/CFS Science Blog
Senior Member (Voting Rights)
Having had a quick look at the original paper, it seems that this measure (sometimes called FInsm5 or spectral fatigue index) is not used very often and was never validated in patient groups. I also haven't found a study that reports it like in the paper by Walitt and colleagues: 'the slope of the Dimitrov Index'. It is usually calculated as the ratio of the -1 and 5th spectral moment and reported as log FInsm5.As @EndME says, do check out that thread on the Dimitrov Index, especially Simon's comment.
Muscle Fatigue during Dynamic Contractions Assessed by New Spectral Indices, 2006, Dimitrov et al.
Strange that the Walitt et al. paper provides no further explanation or background about this measurement, not even in the supplementary material.
Yes, my limited reading suggests the same. There are a range of ways of assessing muscle fatigue, and where the Dimitrov index is used, it seems to be used in conjunction with other measures. It's complicated, but the sense I am getting is that there are enough confounders that the very small sample used in the Walitt study, with very possibly mis-matched controls (mismatched on sex and BMI) as well as the inclusion of the two controls who did not exercise to exhaustion to possibly invalidate the findings.
I've been reading a 2019 PhD thesis by Poyil of the University of Hertfordshire
Usability of upper limb electromyogram features as muscle fatigue indicators for better adaption of human robot interactions
https://core.ac.uk/download/pdf/288394156.pdf
There are some nice basic explanations of what is going on when a muscle is activated.
It's a very interesting field, I believe it could help to identify what is going on in the sensation of muscle fatigue in ME/CFS. Possibly one of the supervisors of Poyil could help look at the raw data from the Walitt study and tell us what might have been happening?
(Dr Amirabdollahian; Dr Steuber). Or someone else who really understands this field.
@Snow Leopard, what do you think? Who do you think might be worth talking to, to evaluate the NIH work, and to try to get excited about doing good studies in ME/CFS?
I think there are lots of decisions that researchers could make to possibly skew things e.g. frequencies looked at, how the data is processed, timepoints included. Muscles that were not being monitored possibly can be recruited in order to help maintain the target force, affecting the identification of the "fatigue" timepoint.
I'm interested to know why the ME/CFS group had a higher mean Dimitrov Index than the controls right at the beginning.
I have only scratched the surface of this and don't have the background to properly critique what was done, but I'm left feeling amazed at the poor quality of so much of the NIH study, including the lack of detail about method. I get a sense of a desire to produce something suggesting 'nothing to see here but a bit of hysteria and effort preference dysfunction, move along quickly'. An electromyogram study, done well, would be a whole paper on its own, not a paragraph in a 'once over lightly and with a handful of people' report.
I've been reading a 2019 PhD thesis by Poyil of the University of Hertfordshire
Usability of upper limb electromyogram features as muscle fatigue indicators for better adaption of human robot interactions
https://core.ac.uk/download/pdf/288394156.pdf
There are some nice basic explanations of what is going on when a muscle is activated.
It's a very interesting field, I believe it could help to identify what is going on in the sensation of muscle fatigue in ME/CFS. Possibly one of the supervisors of Poyil could help look at the raw data from the Walitt study and tell us what might have been happening?
(Dr Amirabdollahian; Dr Steuber). Or someone else who really understands this field.
@Snow Leopard, what do you think? Who do you think might be worth talking to, to evaluate the NIH work, and to try to get excited about doing good studies in ME/CFS?
I think there are lots of decisions that researchers could make to possibly skew things e.g. frequencies looked at, how the data is processed, timepoints included. Muscles that were not being monitored possibly can be recruited in order to help maintain the target force, affecting the identification of the "fatigue" timepoint.
I'm interested to know why the ME/CFS group had a higher mean Dimitrov Index than the controls right at the beginning.
I have only scratched the surface of this and don't have the background to properly critique what was done, but I'm left feeling amazed at the poor quality of so much of the NIH study, including the lack of detail about method. I get a sense of a desire to produce something suggesting 'nothing to see here but a bit of hysteria and effort preference dysfunction, move along quickly'. An electromyogram study, done well, would be a whole paper on its own, not a paragraph in a 'once over lightly and with a handful of people' report.
Jonathan Edwards
Senior Member (Voting Rights)
Disruption of this feedback loop at any level, for example, due to infection of the vagus nerve postulated by VanElzakker [86] to emanate from the gut of ME/CFS, would negatively impact this tightly controlled process and downregulate central nervous system signaling of cardiovascular support peripherally for energy production.
This comment from Keller et al puzzles me. My understanding was that feedback control of muscles is all through the somatic nerves going to the dorsal tracts in the spinal cord rather than through vagal afferents. Quoting a theory of infection of the vagus seems a bit random. I am not sure how damage to vagal afferents would explain the 2 day CPET story. It would more likely show up on day 1 I would think, if it was relevant.
ME/CFS Science Blog
Senior Member (Voting Rights)
Had a look at the results on Motor Evoked Potential (MEP) which is an electrical signal generated in the muscles following stimulation of the brain.The authors tested this during the 30s rest blocks between exercises and describe the result as follows:
In the Samii et al. study, 'post-exercise depression' refers to MEP taken during the recovery period, a couple of minutes after all exercises ended. In all three groups tested (healthy, depressed and CFS) there was a strong decline in MEP with the lowest value being approximately 50% of the pre-exercise MEP value. Samii et al. write: 'postexercise MEP depression was defined as the mean of the lowest MEP amplitudes recorded either 30 seconds, 2 minutes, or 4 minutes into the subject’s recovery period.'
But Samii et al. also tested MEP during the 15s rest periods in between the exercises. Here the MEP increased (rather than decreased) in all three groups. This phenomenon is referred to as post-exercise facilitation. The main finding of the Samii et al. paper was that this facilitation was reduced in the CFS group, while there was no significant difference in post-exercise depression. Here's a graph that shows their results:

I had the impression that Walitt et al. confused post-exercise facilitation and post-exercise depression. Because they measured MEP in between exercise sessions (in the rest periods) rather than minutes after exercise ended (recovery period) they measurement is more similar to the facilitation, not depression in Samii et al.. And so one could say that ME/CFS patients showed a normal response (an increase of MEP) while the values for the controls were unusual?
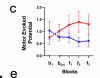
Reference 19 is not about post-exercise depression in healthy and depressed volunteers but reference 20 is (Samii et al. 1996) is. There is, however, a strong difference between the interpretation of Walitt et al and the results reported in this older paper.Motor Evoked Potential amplitudes using transcranial magnetic stimulation of HVs decreased over the course of the task, consistent with post-exercise depression as seen in healthy and depressed volunteers19, while they increased in PI-ME/CFS participants (Fig. 4c). This indicates that the primary motor cortex remained excitable for PI-ME/CFS, suggesting reduced motor engagement from this group20.
In the Samii et al. study, 'post-exercise depression' refers to MEP taken during the recovery period, a couple of minutes after all exercises ended. In all three groups tested (healthy, depressed and CFS) there was a strong decline in MEP with the lowest value being approximately 50% of the pre-exercise MEP value. Samii et al. write: 'postexercise MEP depression was defined as the mean of the lowest MEP amplitudes recorded either 30 seconds, 2 minutes, or 4 minutes into the subject’s recovery period.'
But Samii et al. also tested MEP during the 15s rest periods in between the exercises. Here the MEP increased (rather than decreased) in all three groups. This phenomenon is referred to as post-exercise facilitation. The main finding of the Samii et al. paper was that this facilitation was reduced in the CFS group, while there was no significant difference in post-exercise depression. Here's a graph that shows their results:

I had the impression that Walitt et al. confused post-exercise facilitation and post-exercise depression. Because they measured MEP in between exercise sessions (in the rest periods) rather than minutes after exercise ended (recovery period) they measurement is more similar to the facilitation, not depression in Samii et al.. And so one could say that ME/CFS patients showed a normal response (an increase of MEP) while the values for the controls were unusual?

Last edited:
ME/CFS Science Blog
Senior Member (Voting Rights)
The description for figure 4.c (the one above) is also a bit confusing:
And for the brain activation in Figure 4E they used chronological set of blocks going from 1 to 16. Confusing!
For the graph on the slope of the Dimitrov index (Figure 4.B) they used: 'the first block (b1), the last block prior to fatigue onset (bn), and the first three blocks after fatigue onset (f1, f2, and f3)'. For Figure 4.C they used the same b1, bn, f1,f2,f3 notation but these somehow refer to other blocks, namelijk the last five before fatigue onset.Mean and standard error of the motor evoked potential of HV (blue; n = 6 independent participants) and PI-ME/CFS (red; n = 8 independent participants) participants spanning the last five grip test blocks prior to fatigue onset. The amplitudes of the MEPs of HVs significantly decreased over the course of the task while the amplitudes of the MEPs of PI-ME/CFS participants significantly increased (−0.13 ± 0.2 versus 0.13 ± 0.2 MEP units; t(12) = 2.4, p = 0.03
And for the brain activation in Figure 4E they used chronological set of blocks going from 1 to 16. Confusing!
ME/CFS Science Blog
Senior Member (Voting Rights)
The graph reports the slope, so I assume this refers to the change in Dimitrov Index (DI) values, not the values themselves. So I don't think we know if ME/CFS patients had a higher DI at the beginning.I'm interested to know why the ME/CFS group had a higher mean Dimitrov Index than the controls right at the beginning.
ME/CFS Science Blog
Senior Member (Voting Rights)
By the way: reference 19 is from the same research team (Samii et al. 1997. In this study they tested the amount of exercise needed to induce post-exercise depression in healthy people. Again, it seems that this refers to MEP done during the recovery phase, after exercise ended. The set-up is described as follows:
Post-exercise depression of motor evoked potentials as a function of exercise duration - PubMed (nih.gov)
All the graphs show MEP during the recovery period taking after different lengths of exercise.The subject then performed isometric extension of the right wrist at 50% of MVC for 15 s. Trains of 5 MEPs elicited by 0.3 Hz TMS were recorded from the ECR 30 s and 2 min after the exercise ended, and at 2 min intervals thereafter for 10 min. This procedure was repeated with successive exercise durations of 30, 45, 60, and 90 s. The l0 min period after the end of each exercise was defined as the recovery period.
Post-exercise depression of motor evoked potentials as a function of exercise duration - PubMed (nih.gov)
ME/CFS Science Blog
Senior Member (Voting Rights)
This paper also reports:
Post-exercise depression following submaximal and maximal isometric voluntary contraction - PubMed (nih.gov)studies using functional magnetic resonance imaging (fMRI) have similarly shown that while there is an increase in sensorimotor activation during a fatiguing task (Liu et al., 2003), activation decreases post-fatigue (Benwell et al., 2005)
ME/CFS Science Blog
Senior Member (Voting Rights)
Anyone else had a look at this?I had the impression that Walitt et al. confused post-exercise facilitation and post-exercise depression.
Janna Moen PhD
Established Member
Hey everyone, I finally gathered enough spoons to sort through some of this data myself, and it does not look good.
I ran mixed effect models on the data from 4B and 4C (2way ANOVA cannot handle missing values). 4B had no main effect of block or patient group, and while there was an interaction present, my understanding is that when there is no main effect present, the interaction terms should not be considered.

Similar results for 4C:

Then I tried a regression analysis on the grouped data, this gave results closer to what was reported in the manuscript but still off.
For 4B (Dimitrov Index):

For 4C (MEP amplitude):
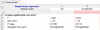
So where did the significant values come from in the manuscript? I did a few different calculations, but it actually seems like they performed individual regressions on each subject, and then used THOSE values (slope of the line) to perform the t-test.
I plotted these out too, and found that apparently, only 2 of the 8 ME/CFS participants had regression slopes that were significantly different from 0:

4C is a similar story with only 1 ME/CFS participant showing a significantly non-zero slope, I don't think I need to paste in another table here but I can if anyone wants.
So when you take the best-fit "slope" values from these individual regressions, we finally get data that mirrors the reported statistical effects:
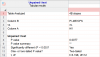
This matches up with the reported effects, with some errors in the order of magnitude of the reported effect size. The p=0.0077 would be rounded up to 0.008, and the t value to 3.2,
The same story is true for 4C:

This also matches up with the reported effects, with a p value rounded down to 0.03 and t=2.4
I'm having a hard time wrapping my brain around this. I don't think I have ever seen a published analysis of this type of data that ran a t-test on individually derived slopes from a study with two dependent variables (patient group and block). This is giving off a lot of red flags RE p-hacking - I find it hard to believe that the NIH team would have jumped to such a convoluted analytical approach organically, especially considering the fMRI data in fig 4E were analyzed correctly using 2-way ANOVA. If I tried to get away with this kind of analysis as a graduate student I would have been rightly roasted by my thesis committee for misrepresenting data.
I'm still considering what to do about this moving forward. I was planning on publishing some of this on my blog and reaching out to Dr. Nath to see what he has to say about it.
I ran mixed effect models on the data from 4B and 4C (2way ANOVA cannot handle missing values). 4B had no main effect of block or patient group, and while there was an interaction present, my understanding is that when there is no main effect present, the interaction terms should not be considered.
Similar results for 4C:
Then I tried a regression analysis on the grouped data, this gave results closer to what was reported in the manuscript but still off.
For 4B (Dimitrov Index):
- Reported data for 4B: 0.2 ± 0.5 versus −0.43 ± 0.3, t(12) = 3.2, p = 0.008
- Simple linear regression in Prism10 for 4B: 0.0003470 ± 0.002101 versus -0.004309 ± 0.001137
For 4C (MEP amplitude):
- Reported data for 4C: −0.13 ± 0.2 versus 0.13 ± 0.2 MEP units; t(12) = 2.4, p = 0.03
- Simple linear regression in Prism10 for 4C: -0.1084 ± 0.07854 versus 0.1451 ± 0.1141
So where did the significant values come from in the manuscript? I did a few different calculations, but it actually seems like they performed individual regressions on each subject, and then used THOSE values (slope of the line) to perform the t-test.
I plotted these out too, and found that apparently, only 2 of the 8 ME/CFS participants had regression slopes that were significantly different from 0:
4C is a similar story with only 1 ME/CFS participant showing a significantly non-zero slope, I don't think I need to paste in another table here but I can if anyone wants.
So when you take the best-fit "slope" values from these individual regressions, we finally get data that mirrors the reported statistical effects:

This matches up with the reported effects, with some errors in the order of magnitude of the reported effect size. The p=0.0077 would be rounded up to 0.008, and the t value to 3.2,
The same story is true for 4C:

This also matches up with the reported effects, with a p value rounded down to 0.03 and t=2.4
I'm having a hard time wrapping my brain around this. I don't think I have ever seen a published analysis of this type of data that ran a t-test on individually derived slopes from a study with two dependent variables (patient group and block). This is giving off a lot of red flags RE p-hacking - I find it hard to believe that the NIH team would have jumped to such a convoluted analytical approach organically, especially considering the fMRI data in fig 4E were analyzed correctly using 2-way ANOVA. If I tried to get away with this kind of analysis as a graduate student I would have been rightly roasted by my thesis committee for misrepresenting data.
I'm still considering what to do about this moving forward. I was planning on publishing some of this on my blog and reaching out to Dr. Nath to see what he has to say about it.
Attachments
I think in a case like this it would be a reasonable request to ask the research team to show exactly what they did with the data and all the calculations and stats tests they did to reach the quoted numerical outcomes. It's not enough to say here's the raw data and here's a p value.
ME/CFS Science Blog
Senior Member (Voting Rights)
Thanks for the analyses @Janna Moen PhD !
I do not have a formal statistical background but will try to comment anyway.
Implementing this in Python, I got different results from you:
from pymer4.models import Lmer
model = Lmer('value ~ block * is_patient + (1|ID)', data=data)
model.fit()

So the p-value for the interaction I got is 0.002 which is not very different from the 0.008 reported in the paper using a t-test. What estimate did you get for the interaction?

What I do find strange is the selection of blocks, which seems to differ for each analysis (figure 4B, 4C or 4E), see:
https://www.s4me.info/threads/grip-...fs-2024-walitt-et-al.37475/page-5#post-542967
It would be better if they made all the data available so that we can check if the conclusion also applies if different blocks were selected.
I do not have a formal statistical background but will try to comment anyway.
I would say it is the interaction that we are interested in here. We want to know how the values of the patients versus controls differed as blocks progressed. Also need to take into account the repeated measurements (some measurements where from the same participants), so use ID as grouping factor (random effect).my understanding is that when there is no main effect present, the interaction terms should not be considered.
Implementing this in Python, I got different results from you:
from pymer4.models import Lmer
model = Lmer('value ~ block * is_patient + (1|ID)', data=data)
model.fit()
So the p-value for the interaction I got is 0.002 which is not very different from the 0.008 reported in the paper using a t-test. What estimate did you get for the interaction?
I assume you did a simple regression: value ~ block for the patient and control group separately? The problem is that this does not take into account the repeated measurements which would remove a lot of the variance.In the 4B dataset at least, the HV regression does not significantly differ from zero, but the PI-ME/CFS group does
Agree, got the same results as you but each participant only had 5 measurements, which makes it difficult to reach statistical significance. So I don't think looking at each participant separately indicates much.I plotted these out too, and found that apparently, only 2 of the 8 ME/CFS participants had regression slopes that were significantly different from 0:

I agree it's unconventional but (at least in my mind) it is conceptionally similar to doing a mixed linear model for the interaction.I don't think I have ever seen a published analysis of this type of data that ran a t-test on individually derived slopes from a study with two dependent variables (patient group and block). This is giving off a lot of red flags RE p-hacking
What I do find strange is the selection of blocks, which seems to differ for each analysis (figure 4B, 4C or 4E), see:
https://www.s4me.info/threads/grip-...fs-2024-walitt-et-al.37475/page-5#post-542967
It would be better if they made all the data available so that we can check if the conclusion also applies if different blocks were selected.
Janna Moen PhD
Established Member
I would say it is the interaction that we are interested in here. We want to know how the values of the patients versus controls differed as blocks progressed. Also need to take into account the repeated measurements (some measurements where from the same participants), so use ID as grouping factor (random effect).
Ah, so I definitely was mixing up my stats principles here (it's been a long time....). I was thinking of situations in which multiple comparisons analyses are run without a significant interaction, which is the actual statistical no-no. An interaction without any main effects just indicates a crossover interaction, which we do see in both graphs. This was helpful: https://www.theanalysisfactor.com/interactions-main-effects-not-significant/
So the p-value for the interaction I got is 0.002 which is not very different from the 0.008 reported in the paper using a t-test. What estimate did you get for the interaction?
So I think this is one of the limitations of GraphPad Prism, I don't think it supports linear mixed models, at least not that I can find with the software. So the regression analysis I did isn't actually capable of comparing the two and doesn't generate a p-value. Your approach is definitely more appropriate so I'm glad the p-value was closer to what they reported.
Agree, got the same results as you but each participant only had 5 measurements, which makes it difficult to reach statistical significance. So I don't think looking at each participant separately indicates much.
Agreed, which is why I think it's strange they chose to analyze the data by just calculating regression slopes for each individual. These relationships don't seem to be straightforwardly linear, the R2 values from the simple individual regressions were all over the place. I wonder if other similar data are typically analyzed this way? I would like to dig into this more when I have the time/energy.
What I do find strange is the selection of blocks, which seems to differ for each analysis (figure 4B, 4C or 4E), see:
https://www.s4me.info/threads/grip-...fs-2024-walitt-et-al.37475/page-5#post-542967
That is a very good observation, I had not spotted the discrepancy in the figure legend RE using the "last five blocks before fatigue onset". I think this is either an error that the editorial team missed, or they mislabeled the blocks in 4C. What I think is even more problematic about this analysis is that several of the HVs never reached the fatigue threshold and they were not required to continue the task until fatigue set in, so this analysis isn't as standardized as it seems. It seems like a strange oversight in the study protocol.
I also agree that the method they used to bin the blocks in 4E is inappropriate - 6/7 ME/CFS participants were fatigued by block 10, while 5/6 controls were still unfatigued at block 15. The fact that there is a significant difference in TPJ activity between groups in blocks 9-12 and 13-16 therefore should not be surprising and IMO likely reflects something about the fatigued state in ME vs HVs. fMRI data is quite messy and with such a small sample size I'm sure it was difficult to get interpretable results without binning, but it might have been nice to see them compare i.e. first 4 non-fatigued blocks vs 4 blocks following fatigue onset.
Their whole speculation about TPJ functioning as a "mismatch" detector is also based off of a single hypothesis paper from 2022 that, as far as I can tell, has no direct empirical support. Coming up with potential theories and models from fMRI data is big part of cognitive neuroscience, there is a lot of value to that kind of analysis, but I find it disingenuous to present it as if it is established fact when it is, in fact, speculation.
Attachments
Their whole speculation about TPJ functioning as a "mismatch" detector is also based off of a single hypothesis paper from 2022 that, as far as I can tell, has no direct empirical support. Coming up with potential theories and models from fMRI data is big part of cognitive neuroscience, there is a lot of value to that kind of analysis, but I find it disingenuous to present it as if it is established fact when it is, in fact, speculation.
There's also the potentially major confounder given developing evidence of global cerebral blood flow (and oxygen extraction fraction) being abnormal in ME/LC. All fMRI studies in this patient group may be uninterpretable.
Janna Moen PhD
Established Member
There's also the potentially major confounder given developing evidence of global cerebral blood flow (and oxygen extraction fraction) being abnormal in ME/LC. All fMRI studies in this patient group may be uninterpretable.
Yes, this is a caveat in every fMRI study but especially so where alterations in cerebral blood flow and neurovascular coupling are suspected. I don't think this means that fMRI shouldn't be used to study ME/CFS but that the results need to be interpreted carefully, good manuscripts will include this kind of potential confounder in the discussion. I really wish they had published these results as smaller and more focused manuscripts that could have expanded on these discussions and framed the results in a better/more accurate context.
Case report (paywall) where HGS was being tested in a healthy volunteer who developed fatigue, weakness, brain fog etc during acute, limited duration covid —
Insights into COVID-19 pathophysiology from a longitudinal multisystem report during acute infection (2024, Experimental Neurology)
Insights into COVID-19 pathophysiology from a longitudinal multisystem report during acute infection (2024, Experimental Neurology)
- we report increased and more bilateral sensorimotor frontoparietal activation during handgrip tasks at V3 despite similar grip force produced during task trials, compared with the other visits
- findings support the idea of a more desynchronized system with potential compensatory neural activations and processes to produce muscular output necessary to maintain “normal” task performance
- a lateralized and more focused activation pattern is often associated with a better synchronization of the descending volley and/or responsiveness of motoneurons to supraspinal input which results in better control of movement and force
- The lower functional connectivity observed at rest could reflect the lower efficiency of the networks during acute COVID-19 infection with less functional communication between regions appertaining at the same network to potentially limit excessive energy consumption at rest.
- lesser focused and more bilateral cortical activation during motor task performance and weaker functional connectivity between frontoparietal regions at rest may reflect less optimal state of the brain during the acute COVID-19 infection and the pathways activity dysregulation, due to the ongoing pathophysiological processes, which could potentially explain the dysexecutive and “brain fog” symptom experienced by COVID-19 individuals
Kitty
Senior Member (Voting Rights)
- findings support the idea of a more desynchronized system with potential compensatory neural activations and processes to produce muscular output necessary to maintain “normal” task performance
- a lateralized and more focused activation pattern is often associated with a better synchronization of the descending volley and/or responsiveness of motoneurons to supraspinal input which results in better control of movement and force
- The lower functional connectivity observed at rest could reflect the lower efficiency of the networks during acute COVID-19 infection with less functional communication between regions appertaining at the same network to potentially limit excessive energy consumption at rest.
This touches on something I've often thought about, but never actually said aloud in an ME forum because it sounds ridiculous.
Microsoft Windows was pretty gruesome when it first came out. I didn't know anything about computers, but a techie friend told me that instead of building it from the ground up, they'd just bolted it on top of DOS. It made it inefficient; Apple Macs with slower processors and less RAM tended to run faster, because the commands were a fraction of the length of those Windows had to use.
I said at the time it often felt like my body was trying to run an operating system like the early versions of Windows. That was nearly 40 years ago, so it's quite fun to read this.

