Cardiopulmonary and metabolic responses during a 2-day CPET in [ME/CFS]: translating reduced oxygen consumption [...], Keller et al, 2024

Let's see if this holds going the other way. Instead of percent change from day 1 to day 2 based on day 1, I got the percent change from day 2 to day 1 based on day 2:



Yes, so pretending day 2 is day 1, ME/CFS will have the super high outliers going in reverse too, because they have the lowest AT on day 2 as well. In this case, there's a single blue with the nine reds in the >100% outlier group.

Edit: This only affects the percentage change that we are looking at. All the studies have focused on absolute change, which has the more obvious reason ME/CFS doesn't seem to decrease as much that I mentioned. There's not as far down to go.


And would you look at that. The higher their day 1 workload, the greater their decrease. And the blues make up the highest spots.

Pearson correlation is -0.38 with a p-value of 1.5e-6. Spearman is -0.34 with p-value of 2.2e-5.

Edit: Significant for both groups by themselves as well:
HC: PearsonRResult(statistic=-0.47726530494758557, pvalue=2.573080560882015e-05)
MECFS: PearsonRResult(statistic=-0.39724390980517693, pvalue=0.00020047296439091046)

---

So it looks to me like people with ME/CFS have a nearly significant difference for workload change, not because they are more deconditioned, but in spite of being more deconditioned.

Edit: Also, that chart above matches all this surprisingly well. Regression lines for each group are parallel, with the ME/CFS line about 10 watts lower than HC, which suggests that if you control for day 1 workload, ME will decrease 10 watts more (on average).

 

So why does ME/CFS have a lower workload at AT? Is it deconditioning? Do the groups need to be better matched for deconditioning, not to show if the effect still exists, but instead to make the effect clearer?

I tried looking to see if there was a correlation using means from all studies between day 1 AT workload and absolute workload change.

Not really that I can see for everyone combined. I was expecting all the lines to maybe look like the red line. Controls seem to be doing the opposite of my hypothesis (though not significant, unlike for individuals in Keller where it is significant and going down.) Percentage chart looks pretty similar to this absolute chart.

 

Conceptually I find it difficult to see why a low value on day1 would make it easier to have a large percentage increase.

The way I see it each participant has a hypothetical mean, the average value they would get if they were tested infinite times. There will be some variation around that mean but this should be the same for everyone, regardless of ow big your average value is in absolute terms. So it shouldn't cause differences between ME/CFS patients and controls.

If you take the lowest values on day1, then I assume chances are higher that they are below their own personal average value than for someone in the middle or higher end. But this should be the same in both groups.

If you were to remove the 4 outliers from this graph, I don't think it would look that much different for both groups, except that HC have a higher mean for day1 values.

 

Here's what I'm thinking.

First, if you remove the outliers, the percentage chart still looks like it flares out going down towards lower day one workloads. The relationship still seems to exist that you'll see more extreme changes at lower workloads.

That said, I don't see why they should be removed. They look like they fit very well with the rest of the points into the "flaring out" distribution. It doesn't look like anything is wildly abnormal in this graph about these four results specifically.

Second, the why isn't as important as the what. What we're seeing is that there's either something unique about ME/CFS or about people with low day one workloads that allows them to have very large increases. Seeing as the four outliers are only found in the lowest zone of day one workloads, I think it's the latter. I think if we saw more controls with sub-30 workloads, we'd see more controls as outliers.

Speculation on the why:

Option 1: Maybe "percent change" doesn't really work with this for some reason. Maybe variation on CPETs is more "absolute". Whether you can achieve a workload of 50 or 150, your personal random variation will be ±50 watts, not ±50%.

We see that with the absolute changes chart, it looks a lot more "behaved". No outliers, just what appears to be a somewhat strong linear relationship.

Option 2: Maybe lower results on day one workload correlate to muscles which have a harder time maintaining a constant pedal rate, so we'd see bigger swings. Maybe weak muscles explain both of those.

 

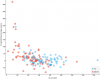
I totally wasted too much time on this, but I found out you can make animations in MatPlotLib, so I had to try this. I animated that graph of day 1 workload vs change in workload from a few posts up and show how it changes if you normalize the change value based on the day 1 value. Basically making the regression lines horizontal.

I didn't even write any of the code myself, it was pretty much 100% AI, but it still took over 5 hours of telling it to tweak things to get it to work correctly.

It's a GIF that might be kind of a large file size (~2 MB) for people with slow internet, so click the thumbnail if you want to view it.


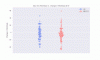
Anyway, the important part, the statistics, took a few minutes.

How I normalized the values: First I got the slopes of the two regression lines for ME/CFS and HC from the plot above of D1_AT_wkld vs AT_wkld_diff_absolute. Since the lines for the groups are independently calculated, and yet pretty much parallel, I think there's a good chance they represent close to the true real world slope of how day 1 workload affects how much your workload will change on the next test, at least for fairly sedentary people, which both groups were. Since they're not exactly the same slope, I got the average of the two, which came out to about -0.3274.

To normalize the change value, I subtracted (-0.3274*D1_wkld) from the change. This makes it so that the regression lines are just about horizontal, so that individuals with different day 1 workloads can now be compared since they aren't sloping towards greater decreases if they start with higher values, which healthy controls were.

Here's the original and the normalized data with the regression lines, same as in the GIF:



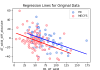
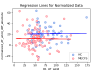
And here are the groups side by side before and after normalization:



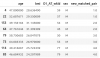
And now the statistical tests. Using normalized change, I get p values less than 0.001. Cohen's d effect size is 0.535.

Again the equation for normalization is:

Code:

normalized_AT_wkld_diff_absolute = AT_wkld_diff_absolute - (-0.3274*D1_AT_wkld)

And that -0.3274 number is just the slope of the line halfway between the blue and red line above.



To try to explain it in simpler terms, there appears to be a trend where the higher the workload on day one of these participants, the more they decreased on day two. The same trend in both groups: for every one watt higher they worked on day one before hitting anaerobic threshold, they, on average, decreased about 0.33 watts more on the next day.

So now imagine you have a person with ME/CFS that gets 50 watts on day one and decreases by 5 points the next day, and a healthy person that gets 70 watts on day one and decreases by 7 points. It looks like the healthy person decreased more than the person with ME.

But wait. The healthy person, just on account of the trend we saw previously, is expected to decrease 0.33 more for every watt higher they started than the other participant. So they started 70 - 50 = 20 watts higher on day one. 20 * 0.33 = 6.6 watts. They would be expected to decrease 6.6 watts more than the other person. But they only decreased 2 watts more. Which suggests that either the healthy person isn't decreasing as much as you would expect, or the person with ME/CFS is decreasing more.

What the normalization equation above is doing is simply subtracting the extra "change" watts that participants are expected to decrease just from starting out higher. Put them on level footing so we can compare the difference in watts changed that is actually interesting. So with the example of the two people above, you would subtract 0.33 times the number of watts they started at from how much they changed:

ME: 50*0.33 watts subtracted from 5 = increase of 11.5 watts.
HC: 70*0.33 watts subtracted from 7 = increase of 16.1 watts

The actual increase values by themselves aren't important, it's comparing between them. We could subtract both by a constant like 16.1 watts if we assume the healthy person's value is normal to get the numbers looking prettier.

Anyway, what we see is that if we don't count the extra watts a person will decrease just from starting higher, the example person with ME decreased 4.6 watts more (or increased 4.6 watts less) than expected for some reason.

So that's basically what I see in the real study data above. When I take away those extra free "change watts" from every participant, which is what's happening with skewing the graphs, the ME participants decreased 9 watts more than the controls on average. (You can see the means of the two groups using normalized data in the statistical test screenshot above.)

Of course, there might not be a real correlation. Or there is, but the real slope of the real world effect is different from what the slope of the study's data looks like, which is about 0.33, and what I'm basing this on.

I only think it's a real effect, as well as close to 0.33, because both groups individually have that same slope (or very near it), and the correlation is significant in both groups.

So the upshot is that I think, based on these results, if you compared two groups with similar workloads on day one, you would see a significantly greater decrease in the ME group. Or if you used this normalization equation for dissimilar groups, you would still see a greater decrease in the ME group.

----

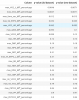
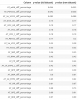
Edit: Slopes and confidence intervals for the two groups:
ME/CFS: -0.338, 95% CI [-0.510, -0.165]
Controls: -0.317, 95% CI [-0.457, -0.177]

 

Published a blog today, summarizing the data and analyses made here:
https://mecfsskeptic.com/the-biggest-2-day-exercise-study/

https://twitter.com/user/status/1836349009037808108

 

Conclusion
In conclusion, the largest and highest quality study on 2-day exercise testing did not find strong evidence of impaired recovery in ME/CFS patients. This suggests that the effects are smaller than initially thought and that the procedure has difficulty in accurately differentiating patients and controls. The data, however, are consistent with a small to moderate effect for VO2 Peak and perhaps for Workload AT as well, depending on how you analyze the data and handle outliers.

In a future blog post, we will take a closer look at previous studies of 2-day exercise testing in ME/CFS patients.

Acknowledgments
Many thanks to forestglip on the Science for ME forum whose thoughtful analysis was very helpful in understanding the Keller et al. dataset.

The following dataset was used from www.mapmecfs.org: Keller et al. Cardiopulmonary and metabolic responses during a 2-day CPET in ME/CFS. Last updated: September 12, 2024, 4:29 PM (UTC+02:00).

 

Maybe that should be its own thread. I'm sure a lot of the forum members have tuned out of our long discussion in this thread by now, and might miss your blog.

 

I made a first attempt at making a workload at AT matched dataset, as opposed to the study's VO2 max matched dataset. I don't know if there's some specific algorithm for doing this task, but an AI's idea was a NearestNeighbors algorithm to find matching pairs at close distances based on sex, bmi, age, and day one workload at AT. It does work, and the pairs look pretty good, I just think a better implementation could get a larger dataset than this crude version. I only got 21 pairs vs the study's 55 pairs. Example pairings of the first few rows:



And here are the workloads in the new matched set:



And absolute and percentage differences:


But anyway, even with only 21 ME/CFS and 21 controls, but now matched for day one workload, the two day difference in workload at AT, both absolute and percent, is significant:



Getting fairly small p-values (~0.01) and pretty large effect sizes (~0.7).

I'll add the code I used to make the dataset as an attachment to verify I didn't hand select rows to make this work. Though note I did first try this with larger thresholds (distance that two participants' values can be from each other) first, and the p-values were larger (around 0.5 to 0.7). The above data is from a threshold of 0.5.
(The only participant excluded in the input csv is PI-026.)

I also tried matching only based on day one workload, and not caring about BMI or age (in the attached code, I removed "bmi" and "age" from "matching features" and lowered threshold to 0.3 to get even closer matching), and the p-values are even lower (<0.01 for percentage):


Day one workload and difference between days in this larger dataset:


Edit: I changed the attached script so that you can just use the raw datafile from mapmecfs as input. Just put the script in the same directory as the dataset, or change the path in the script, and after running, it will create an identical TSV but with a new column called new_matched_pair. Should be identical participants to the ones in this post. Threshold and columns to match on can be changed if desired.

 

I don't know either. I was wondering how they did this - perhaps they recruited controls with the intention to match patients. Anyway, interesting analysis.

Ok thanks, I've posted it here:
https://www.s4me.info/threads/the-biggest-2-day-exercise-study-blog-me-cfs-skeptic.40267/

 

It looks like they updated the data on mapmecfs. Only PI-026's values were changed, and only metrics on day one. (And the value for OUES was moved from rest to AT for every participant.)

VO2 at max and workload at AT on day one are lower now, meaning they had an increase on the second day. I did Mann-Whitney on the new data, it's just a little less significant for those two:



Edit: Reuploaded the images. I forgot to include the column names in the screenshot before.

 

So I found out R actually has a library/function for matching participants called matchit().

I tried it out, matching on age, bmi, and day one workload at AT. There are a lot of different parameters and methods for matching that I haven't explored, but this seems to work well. It's just matching rows where the values are within the specified amount of standard deviations (e.g. 0.5 for D1_AT_wkld in the following code).

Code:

# Find matches. Set caliper values to max SD that rows in matched pairs can differ.
m.out3 <- matchit(phenotype ~ bmi + age + D1_AT_wkld,
                  data = diff_df,
                  method = "nearest", distance = "mahalanobis",
                  exact = ~ sex,
                  caliper = c(bmi = 1, age = 1, D1_AT_wkld = .5))

With the code above, I made a dataset of 46 participants in each cohort.

It also makes cool summaries and plots to visualize the matching. For example, here are the density plots for these features before and after creating a matched set. A lot more similar after matching.


Unadjusted p values aren't anything super special, though. 0.036 for AT_wkld_diff_pct. 0.072 for AT_wkld_diff_abs. >0.6 for the VO2 max percent and absolute diffs.

Here are all 120 p-values for all absolute and percent differences. Apologies for the extremely long image.


In case anyone wants to try the code, I put it on GitHub. Just make sure the three libraries listed at the top are installed, set the path to the mapmecfs tsv file in the file_path variable at the top, and the rest of the script should do everything, including matching up pairs, Mann-Whitney on all features, and exporting the results as an image.

 

Interesting. I was curious to know how it worked so had a look at the code:
https://github.com/kosukeimai/MatchIt/blob/master/R/matchit.R

It's a far too complex for me but if I understand the gist of it, the default is to use logistic regression, calculate predicted values and then find the control participant that has the closest predicted value for each of the patients (the smallest absolute diff in predict values). Something like that?

I'm finding that R has a lot more options for statistics than python. The difference is larger than I expected so I'm thinking about switching back to R again (even though I find it less intuitive).

 

I don't know the details well either, that might be part of it, but there are lots of different options for method that all produce different results, so it's probably a bit more complicated than that. I think that "mahalanobis" in the code above looks for the distances between two points considering all variables listed, but factors in how correlated any two variables are to give a better result somehow, as opposed to a simple euclidean distance.

Propensity score matching seems to be the encompassing term for what this function can do. I saw it was used for controlling for many variables in this study posted on S4ME a few days ago, I looked up what it was, and realized it's the thing I was wondering about here.

Yeah, I have a lot more experience in Python, so I keep trying to do things there, but R keeps having functions for statistics that Python doesn't. For the above, Python has a much simpler version called psmpy, and R ended up having this, which feels much more like a finished, fully featured product.

I think once I'm used to the syntax, stats will be much easier in R though, since that's basically what it's made for, whereas Python is like an all-in-one tool.

I'd recommend RStudio, if you don't use that already. Makes coding a million times easier. I'm working through this data science course on Coursera, which uses RStudio. I'm still near the start, but it's been helpful so far. If you want to do it, all ten sub-courses are free, you just have to go to each individually, and click Audit after clicking Enroll.

Edit: Here is a good tutorial for matchit that compares two methods. I ended up using an example from the package docs though.