IiME letter to Mark Baker (NICE) re: CBT & GET as recommended treatments

[Alvin]

I agree about not fighting any issue which isn't rock solid, but I am wary of compromising before it begins.

In theory your correct but when your dealing with people throwing everything you have at them can backfire. I agree with @Jonathan Edwards tailoring his message for his audience, instead of insulting them he is using a framed argument thats easier to persuade them with that benefits us. Remember that this issue can be brought up later or elsewhere but what he is doing is saying here are some flaws and why this study is bogus and its reasons you can relate to. It also never hurts to have more arguments in your back pocket if they are needed but in this case i agree with his approach, In another case i would not.
Think of this as divide and conquer, he is not lying at all but he is being strategic for the audience at hand.

 

[Valentijn]

It starts with patient presenting with profound fatigue.

Profound fatigue is not the same as requiring that fatigue be the principal symptom. "Profound" and "principal" mean very different things.

 

[Trish]

Profound fatigue is not the same as requiring that fatigue be the principal symptom. "Profound" and "principal" mean very different things.

I'm trying to think back to what I 'presented' with to my doctor in the early days. I'm pretty sure I would have told him I felt ill all the time, my muscles were painful and felt like they couldn't function properly, and the more physical activity I did the worse I felt. I don't think I've ever complained of 'fatigue' - in fact I'm not even sure what it means - tired all the time? rapid muscle fatiguability? too vague...

 

[Inara]

If you find ibuprofen works in an unselected population of people with joint pain then you can expect it to work in a patient with RA who has joint pain, unless you have a specific reason to doubt it.

I think here the discussion could go on and on... meaning, in my opinion, your arguments are valid, as the others' are, too.

I think, strictly scientifically, you cannot apply statements/results about joint pain to RA without further steps. Even if it seems logical, obvious or even trivial. We all know that we can be false with our "that's obvious"-feeling. There can be reasons found why you cannot deduce from the one to the other, e.g. the joint pain in RA is not the same joint pain as in joint pain, meaning the joint pain in RA has another origin and/or there are interactions between symptoms/processes leading to another type of joint pain.

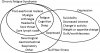
I imagine that in terms of sets and ask myself: Is there a subset? If RA were a true subset of joint pain, then it could be logical to deduce: What works for joint pain, works for joint pain in RA. If RA and joint pain are two sets whose intersection is non-empty (but RA is not a subset), then you only can make that statement for the intersection set.

The question is: What are the elements of the intersection? And is there really an intersection? In case of joint pain (let's make it easy) that intersection could consist of one element: joint pain. Or it is empty.

In case of "chronic fatigue" (set 1) and ME (set 2), set 1 and set 2 might also be distinct, i.e. empty intersection; there could be an intersection: fatigue. Or even more: fatigue and headaches. But it doesn't have to. It depends on your selection of cohort. Furthermore, there will always be elements (symptoms) in set 1 that don't lie in set 2 and vice versa.

In my view it is pretty difficult in this case which characteristics of "chronic fatigue" can be transported to "ME", which yould you need to do in order to say "this or that helps".

 

[Valentijn]

I think, strictly scientifically, you cannot apply statements/results about joint pain to RA without further steps. Even if it seems logical, obvious or even trivial. We all know that we can be false with our "that's obvious"-feeling. There can be reasons found why you cannot deduce from the one to the other, e.g. the joint pain in RA is not the same joint pain as in joint pain, meaning the joint pain in RA has another origin and/or there are interactions between symptoms/processes leading to another type of joint pain.

I think we have a strong argument along these lines regarding most exercise recommendations: "exercise is beneficial in healthy people, ergo it must be beneficial in ME." It requires ignoring that ME patients, by definition, are not normal healthy human beings. This claim can only be propped up by a psychosomatic theory ("you think you are ill, but you are physically healthy"), which is easily knocked down by a great deal of research.

The bigger problem comes with the claim that "exercise is beneficial for people with fatigue, ergo it must be beneficial in ME." How do we argue that ME is not a subset of fatigue, especially with the disease being characterized as chronic fatigue syndrome? Alternatively, how to we argue that ME is a subset of fatigue where the usual rules of fatigue don't apply? I think this is what @Jonathan Edwards has been getting at.

It's hard to argue that objective things like the CPET establish the difference, when it isn't (and can't be) used in any diagnostic criteria. It establishes that the disease is biomedical, but doesn't untangle it from fatigue, nor help distance ME from fatigue treatments.

A more pragmatic argument may be that allowing Oxford to influence treatment has encouraged researchers to continue using vague criteria, when better criteria are available including NICE's own criteria. The current problem may be that Oxford studies of CBT/GET are pretty much all that is available, so even if flawed they offer the only evidence available, and it's therefore better than nothing. But we can argue that enabling the "better than nothing" approach is actively impeding quality research and scientific progress, so must be ended if progress is ever to be made.

 

[Inara]

I didn't realise (IOM) ME was a subset of Oxford but it seems it is.

No, Oxford-CFS is not a superset of ICC-ME.

 

[Inara]

The problem is that dealing with NICE guidance is not about PACE. It's about a bunch of studies, some of which show objective improvements. The ones which show objective improvement use Oxford and have indications that patients were not physically disabled at baseline. How do we argue that those trials are not relevant to ME/CFS, except by arguing that the criteria used did not recruit ME/CFS patients?

Well said!

 

[Inara]

The bigger problem comes with the claim that "exercise is beneficial for people with fatigue, ergo it must be beneficial in ME."

Strictly, one counter-example is enough to falsify a hypothesis.

Hypothesis: Exercise is beneficial in people with fatigue => it is beneficial in ME.

There exists at least on person with ME for whom exercise is not beneficial. I.e. hypothesis is false.

(The reason why the falsification of a hypothesis is not accepted is, in my opinion, the un-willingness to reject a hypothesis even if only one counter-example exists. E.g. statistical arguments arise à la "only one!" But this is how scientists agreed to do science: Reject hypothesis if experiments don't verify it. And it's reasonable.)

Second, strictly, it would have to be proven that "Oxford-fatigue" is equal to "ME-fatigue", meaning equal. This includes showing that both fatigue-types are the result of the same process, plus taking into account interactions. Interestingly, nobody would dare to say that "Oxford-fatigue" is equal to "cancer-fatigue", although both times the word "fatigue" is used.

I know people see me here as a pain in the ass. But science is not about applying some standard scheme (probably incorrectly) and then making (arbitrary) statements. It is about understanding reality. And for this, you need to be exact, even if it sucks. Theoretical physics, for instance, exist due to exactness, because of lack of experiments.

I, too, understand @Jonathan Edwards argument - I hope. Still I think this is an important point which - if thought through in detail - could be a very good argument even in political matters.

 

[Sly Saint]

back to the cbt...............

"This clip contains an excerpt from the DVD "10 Minute CBT in practice: Health anxiety and medically unexplained symptoms". In this scenario, a GP demonstrates simple CBT strategies for managing a patient with chronic fatigue or "tiredness all the time". The 10 Minute CBT DVD series will help busy health professionals learn effective cognitive-behavioural therapy (CBT) strategies to use in a typical primary care consultation. Each brief clip highlights key skills for working with common mental and physical health problems. The training is designed for a wide range of primary care health professionals including GPs, nurses, occupational health, rehabilitation and many others."

10 Minute CBT is a company which, according to its website, does
"Online courses for NHS, commercial and educational organisations that want to promote well being via cognitive behavioural therapy. More."

Note: although it says 'Chronic fatigue', 'tired all the time', the website link takes you to a page (where the video is) entitled 'Chronic Fatigue Syndrome' and on the video it has it across the screen.

the video is also on Youtube.
this is the direct link to it on the 10minute CBT site:
http://www.10minutecbt.co.uk/video-clips/chronic-fatigue-syndrome-10-minute-cbt/

Inclusion under MUS also has to be something else that needs to be raised with NICE.

eta: youtube link

 

[Alvin]

I know people see me here as a pain in the ass.

I don't but i can probably challenge you on the title for that one, i seem to end up in many arguments where most disagree with me.

 

[large donner]

Does anyone remember which other criterias were used in the PACE trial because it wasn't just the Oxford criteria. This is really important as I seem to remember a screening criteria then an another unpublished criteria.

I don't think people are really grasping this in the discussion we are having on this thread.

Don't forget they changed the very definition of pacing in the PACE trial so its not beyond them to do a slight of hand on the claimed criterias used.

I wish I had the brain power to think back to all the critiques at the time but I don't.

I'm pretty sure some people were saying that they used Oxford in such a way to attempt to screen down eventually to a purely tired all the time criteria or at least a cohort that gave that best potential.

Essentially one they believed had the best potential to benefit from their treatments.

 

[Amw66]

Could we not have a venn diagram - perhaps similar to the one in Nature for the differences in cerebrospinalfluid after exercise CFS/GWI/Depression, ( attached) but for the different diagnostic criteria - images are easier to process?
This may help make sense of issues

 

[Graham]

Does anyone remember which other criterias were used in the PACE trial because it wasn't just the Oxford criteria.

They used the London criteria for ME, which is only used, as far as I can see, by some UK researchers. They found that half of those who qualified under the Oxford criteria satisfied the London criteria, so as a glib measure (assuming London defines ME) around half the folk satisfying Oxford have ME. What we don't know is how many patients considered for the trial failed the Oxford criteria but would have satisfied the London criteria.

Another puzzle is why they needed to start with 3158 patients to end up with a sample of 641 eligible for the trial. Some reasons for exclusion were good (poor English, for example): around 600 declined to take part: 1088 did not meet Oxford criteria: a number (diagnosed with Oxford CFS) were less severely affected, so were excluded (their scores subsequently would be taken to mean that they had recovered). But this is a trial on treatment offered to folk sent to ME centres. It's true that Newcastle and one of the London ME centres reported that around half the people sent to them did not have ME, but another undiagnosed complaint (such as sleep apnoea), but this is only 20% of the patients turning up at the centres.

 

[Invisible Woman]

Does anyone remember which other criterias were used in the PACE trial because it wasn't just the Oxford criteria. This is really important as I seem to remember a screening criteria then an another unpublished criteria.

Yeah. I remember Wessely saying somewhere that they had to broaden the scope otherwise no one would have recovered. But was that about criteria of about lowering thresholds.

Your post is ringing bells,but I can't quite remember either

 

[Alvin]

Yeah. I remember Wessely saying somewhere that they had to broaden the scope otherwise no one would have recovered

That makes me mad, its basically an admission that they are peddling lies but must rewrite the rule book to invent the numbers they want to punish us with.

 

[large donner]

Some reasons for exclusion were good (poor English, for example): around 600 declined to take part: 1088 did not meet Oxford criteria:

If the Oxford Criteria (an all encompassing fatigue criteria) is just a principal complaint of fatigue exactly how could anyone not meet the criteria.

Is it being claimed that those people didn't have fatigue, or they did have fatigue but they also had more than just fatigue therefore they were over qualified for the criteria, for example, if they had PEM?

 

[Guest 102]

If the new NICE guideline does not explicitly state that over exertion can be extremely harmful for ME patients then it is frankly not fit for purpose.

 

[Valentijn]

Is it being claimed that those people didn't have fatigue, or they did have fatigue but they also had more than just fatigue therefore they were over qualified for the criteria, for example, if they had PEM?

I don't think they clarified, but it could happen if another symptom was more prominent than fatigue. I doubt they would usually exclude patients from clinics on that basis, but they probably find it useful in research.

 

[Alvin]

I remember Wessely saying somewhere that they had to broaden the scope otherwise no one would have recovered.

If we can find a recording/transcript of this it would be good for future confrontations.

 

[Indigophoton]

If the Oxford Criteria (an all encompassing fatigue criteria) is just a principal complaint of fatigue exactly how could anyone not meet the criteria.

The Oxford Criteria has a number of exclusions, for example, anaemia and schizophrenia. Presumably 1088 people had conditions which prevented them from being included.

And/or, their fatigue did not meet Oxford requirements, eg, was not present at least 50% of the time etc.